About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 1184 results for "Lee-Ann Sutherland" clear search
Unification-Conditions-of-Civilization-Patterns-Multi-Agent-Modeling-of-Human-History
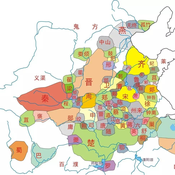
zhuo zhang | Published Friday, May 27, 2022 | Last modified Sunday, May 29, 2022The model of Chinese and Western civilization patterns can help understand how civilizations formed, how they evolved by themselves, and the difference between the unity of China and the disunity of the Western. The previous research had examined historical phenomena about civilization patterns with subjective, static, local, and inductive methods. Therefore, we propose a general model of history dynamics for civilizations pattern, which contains both China and the West, to improve our understanding of civilization formation and the factors influencing the pattern of civilization. And at the same time, the model is used to find the boundary conditions of two different patterns.
Correlated random walk
Thibault Fronville | Published Friday, April 01, 2022 | Last modified Monday, April 25, 2022The first simple movement models used unbiased and uncorrelated random walks (RW). In such models of movement, the direction of the movement is totally independent of the previous movement direction. In other words, at each time step the direction, in which an individual is moving is completely random. This process is referred to as a Brownian motion.
On the other hand, in correlated random walks (CRW) the choice of the movement directions depends on the direction of the previous movement. At each time step, the movement direction has a tendency to point in the same direction as the previous one. This movement model fits well observational movement data for many animal species.
The presented agent based model simulated the movement of the agents as a correlated random walk (CRW). The turning angle at each time step follows the Von Mises distribution with a ϰ of 10. The closer ϰ gets to zero, the closer the Von Mises distribution becomes uniform. The larger ϰ gets, the more the Von Mises distribution approaches a normal distribution concentrated around the mean (0°).
This model is implemented in python and can be used as a building block for more complex agent based models that would rely on describing the movement of individuals with CRW.
FeedUS - A global food trade model
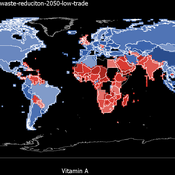
Jiaqi Ge | Published Thursday, February 25, 2021 | Last modified Friday, February 26, 2021The purpose of the model is to study the impact of global food trade on food and nutrition security in countries around the world. It will incorporate three main aspects of trade between countries, including a country’s wealth, geographic location, and its trade relationships with other countries (past and ongoing), and can be used to study food and nutrition security across countries in various scenarios, such as climate change, sustainable intensification, waste reduction and dietary change.
Peer reviewed Multilevel Group Selection I
Wayne W. Wakeland Thaddeus Shannon Garry Sotnik | Published Tuesday, April 21, 2020 | Last modified Saturday, July 03, 2021New theoretical agent-based model of population-wide adoption of prosocial common-pool behavior with four parameters (initial percent of adopters, pressure to change behavior, synergy from behavior, and population density); dynamics in behavior, movement, freeriding, and group composition and size; and emergence of multilevel group selection. Theoretical analysis of model’s dynamics identified six regions in model’s parameter space, in which pressure-synergy combinations lead to different outcomes: extinction, persistence, and full adoption. Simulation results verified the theoretical analysis and demonstrated that increases in density reduce number of pressure-synergy combinations leading to population-wide adoption; initial percent of contributors affects underlying behavior and final outcomes, but not size of regions or transition zones between them; and random movement assists adoption of prosocial common-pool behavior.
Agent-based model of power dynamics in agri-food systems
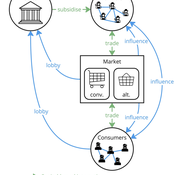
Tim Williams | Published Sunday, October 27, 2024 | Last modified Thursday, June 12, 2025This is a stylised agent-based model designed to explore the conditions that lead to lock-ins and transitions in agri-food systems.
The model represents interactions between four different types of agents: farmers, consumers, markets, and the state. Farmers and consumers are heterogeneous, and at each time step decide whether to trade with one of two market agents: the conventional or alternative. The state agent provides subsidies to the farmers at each time step.
The key emergent outcome is the fraction of trade in each time step that flows through the alternative market agent. This arises from the distributed decisions of farmer and consumer agents. A “sustainability transition” is defined as a shift in the dominant practices (and associated balance of power) towards the alternative paradigm.
…
Equity Constrained Dispatching Model of Emergency Medical Services
Sreekanth V K Ram Babu Roy | Published Thursday, September 08, 2016 | Last modified Monday, May 01, 2017Model for evaluating various ambulance dispatching policies of an equity constrained emergency medical services under bounded rationality.
Peer reviewed Deforestation
MohammadAli Aghajani | Published Saturday, January 20, 2024 | Last modified Thursday, August 14, 2025Deforestation Simulation Model in NetLogo with GIS Layers
This model has developed in Netlogo software and utilizes
the GIS extension.
This NetLogo-based agent-based model (ABM) simulates deforestation dynamics using the GIS extension. It incorporates parameters like wood extraction, forest regeneration, agricultural expansion, and livestock impact. The model integrates spatial layers, including forest areas, agriculture zones, rural settlements, elevation, slope, and livestock distribution. Outputs include real-time graphical representations of forest loss, regeneration, and land-use changes. This model helps analyze deforestation patterns and conservation strategies using ABM and GIS.
Diffusion dynamics in small-world networks with heterogeneous consumers
Sebastiano Delre | Published Saturday, September 10, 2011 | Last modified Saturday, April 27, 2013This model simulates diffusion curves and it allows to test how social influence, network structure and consumer heterogeneity affect their spreads and their speeds.
Agent-Based Computational Modeling of Cryptocurrency Design
Felix Ude | Published Friday, June 28, 2019Agent-Based Computational Model of the cryptocurrency Bitcoin with a realistic market and transaction system. Bitcoin’s transaction limit (i.e. block size) and Bitcoin generation can be calibrated and optimized for wealth and network’s hashing power by the Non-Dominated Sorted Genetic Algorithm - II.
Agent-based model for centralized student admission process
Connie Wang Shu-Heng Chen Bin-Tzong Chi | Published Wednesday, November 04, 2015 | Last modified Wednesday, March 06, 2019This model is to match students and schools using real-world student admission mechanisms. The mechanisms in this model are serial dictatorship, deferred acceptance, the Boston mechanism, Chinese Parallel, and the Taipei mechanism.
Displaying 10 of 1184 results for "Lee-Ann Sutherland" clear search