About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 810 results for "Jon Solera" clear search
Crowdworking Model
Georg Jäger | Published Wednesday, September 25, 2019The purpose of this agent-based model is to compare different variants of crowdworking in a general way, so that the obtained results are independent of specific details of the crowdworking platform. It features many adjustable parameters that can be used to calibrate the model to empirical data, but also when not calibrated it yields essential results about crowdworking in general.
Agents compete for contracts on a virtual crowdworking platform. Each agent is defined by various properties like qualification and income expectation. Agents that are unable to turn a profit have a chance to quit the crowdworking platform and new crowdworkers can replace them. Thus the model has features of an evolutionary process, filtering out the ill suited agents, and generating a realistic distribution of agents from an initially random one. To simulate a stable system, the amount of contracts issued per day can be set constant, as well as the number of crowdworkers. If one is interested in a dynamically changing platform, the simulation can also be initialized in a way that increases or decreases the number of crowdworkers or number of contracts over time. Thus, a large variety of scenarios can be investigated.
Peer reviewed Minding Norms in an Epidemic Does Matter
Klaus G. Troitzsch | Published Saturday, February 27, 2021 | Last modified Monday, September 13, 2021This paper tries to shed some light on the mutual influence of citizen behaviour and the spread of a virus in an epidemic. While the spread of a virus from infectious to susceptible persons and the outbreak of an infection leading to more or less severe illness and, finally, to recovery and immunity or death has been modelled with different kinds of models in the past, the influence of certain behaviours to keep the epidemic low and to follow recommendations of others to apply these behaviours has rarely been modelled. The model introduced here uses a theory of the effect of norm invocations among persons to find out the effect of spreading norms interacts with the progress of an epidemic. Results show that norm invocations matter. The model replicates the histories of the COVID-19 epidemic in various region, including “second waves” (but only until the end of 2021 as afterwards the official statistics ceased to be reliable as many infected persons did not report their positive test results after countermeasures were relieved), and shows that the calculation of the reproduction numbers from current reported infections usually overestimates the “real” but in practice unobservable reproduction number.
The Urban Drought Nexus Tool
Roger Cremades Muhamad Khairulbahri | Published Thursday, December 14, 2023The “Urban Drought Nexus Tool” is a system dynamics model, aiming to facilitate the co-development of climate services for cities under increasing droughts. The tool integrates multiple types of information and still can be applied to other case studies with minimal adjustments on the parameters of land use, water consumption and energy use in the water sector. The tool needs hydrological projections under climate scenarios to evaluate climatic futures, and requires the co-creation of socio-economic future scenarios with local stakeholders. Thus it is possible to provide specific information about droughts taking into account future water availability and future water consumption. Ultimately, such complex system as formed by the water-energy-land nexus can be reduced to single variables of interest, e.g. the number of events with no water available in the future and their length, so that the complexities are reduced and the results can be conveyed to society in an understandable way, including the communication of uncertainties. The tool and an explanatory guide in pdf format are included. Planned further developments include calibrating the system dynamics model with the social dynamics behind each flow with agent-based models.
Online Protest and Repression in Authoritarian Settings (OPRAS)
Nanda Wijermans Annie Waldherr Aytalina Kulichkina | Published Tuesday, January 27, 2026This agent-based model, developed for the study “Online Protest and Repression in Authoritarian Settings,” examines how online protest and repression evolve in authoritarian contexts and how these dynamics affect ordinary users’ attitudes and behavior on social media. The model integrates key theoretical and empirical insights into social media use and core political factors that shape digital contention in authoritarian settings. The following questions are addressed: (1) how online protest–repression dynamics unfold across different levels of authoritarianism and varying compositions of committed accounts, and (2) how ordinary users’ internal propensity to protest and their perceived probability of successful repression change during online protest-repression contestation. The model is evaluated against two empirically grounded macro patterns observed in the real world. The first is enduring protest: online protest becomes dominant as vocal protesters grow to outnumber vocal repressors, shrinking the pool of silent users and stabilizing a pro-protest majority. The second is suppressed protest: online dissent is contained as vocal repression and silence expand in response to protest, yielding a sustained majority of repressive and silent accounts. Together, these dynamics demonstrate how dissenting voices are empowered and suppressed online in authoritarian settings.
01a ModEco V2.05 – Model Economies – In C++
Garvin Boyle | Published Monday, February 04, 2013 | Last modified Friday, April 14, 2017Perpetual Motion Machine - A simple economy that operates at both a biophysical and economic level, and is sustainable. The goal: to determine the necessary and sufficient conditions of sustainability, and the attendant necessary trade-offs.
Asymmetric two-sided matching
Naoki Shiba | Published Wednesday, January 09, 2013 | Last modified Tuesday, May 28, 2013This model is an extended version of the matching problem including the mate search problem, which is the generalization of a traditional optimization problem. The matching problem is extended to a form of asymmetric two-sided matching problem.
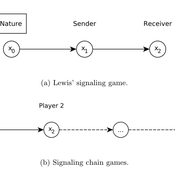
Lewis' Signaling Chains
Giorgio Gosti | Published Wednesday, January 14, 2015 | Last modified Friday, April 03, 2015Signaling chains are a special case of Lewis’ signaling games on networks. In a signaling chain, a sender tries to send a single unit of information to a receiver through a chain of players that do not share a common signaling system.
Private forest owner management behavior using social interactions, information flow, and peer-to-peer n
Jessica Leahy Emily Silver Huff Aaron R Weiskittel Caroline L Noblet David Hiebeler | Published Tuesday, October 13, 2015This theoretical model includes forested polygons and three types of agents: forest landowners, foresters, and peer leaders. Agent rules and characteristics were parameterized from existing literature and an empirical survey of forest landowners.
Coastal Coupled Housing and Land Markets (C-CHALMS)
Nicholas Magliocca | Published Thursday, May 18, 2017Next generation of the CHALMS model applied to a coastal setting to investigate the effects of subjective risk perception and salience decision-making on adaptive behavior by residents.
Hyperconnectivity, and Fact-Checking- Modeling Witnessing as a Traditional Coast Salish Mechanism
Adam Rorabaugh | Published Thursday, May 01, 2025An unintended consequence of low cost maritime travel may be hyperconnectedness, creating social situations where information can be readily passed before it is verified- an issue not limited to modern digitally connected societies. In traditional Coast Salish societies, the peoples of what is now Western Washington and Southwestern British Columbia, oral traditions were vertified through a process called witnessing. Witnesses would be trained to recount and verify oral history and traditional teachings at high fidelity. Here, a simple model based on dual inheritance approaches to genes and culture, is used to compare this specific form of verifying socially important information compared to modern mass communication. The model suggests that witnessing is a high fidelity form of transmitting knowledge with a low error rate, more in line with modern apprenticeships than mass communication. Social mechanisms such as witnessing provide solutions to issues faced in contemporary discourse where the validity of information and even fact checking mechanisms may be biased or counterfactual. This effort also demonstrates the utillity of using modeling approaches to highlight how specific, historically contingent institutions such as witnesses can be drawn upon to model potential solutions to contemporary issues solved in the past in traditional Coast Salish practice.
Displaying 10 of 810 results for "Jon Solera" clear search