The model represents a team intended at designing a methodology for Institutional Planning. Included in ICAART’14 to exemplify how emotions can be identified in SocLab; and in ESSA’14 to show the Efficiency of Organizational Withdrawal vs Commitment.

This is a model of organizational behavior in the hierarchy in which personnel decisions are made.
The idea of the model is that the hierarchy, busy with operations, is described by such characteristics as structure (number and interrelation of positions) and material, filling these positions (persons with their individual performance). A particular hierarchy is under certain external pressure (performance level requirement) and is characterized by the internal state of the material (the distribution of the perceptions of others over the ensemble of persons).
The World of the model is a four-level hierarchical structure, consisting of shuff positions of the top manager (zero level of the hierarchy), first-level managers who are subordinate to the top manager, second-level managers (subordinate to the first-level managers) and positions of employees (the third level of the hierarchy). ) subordinated to the second-level managers. Such a hierarchy is a tree, i.e. each position, with the exception of the position of top manager, has a single boss.
Agents in the model are persons occupying the specified positions, the number of persons is set by the slider (HumansQty). Personas have some operational performance (harisma, an unfortunate attribute name left over from the first edition of the model)) and a sense of other personas’ own perceptions. Performance values are distributed over the ensemble of persons according to the normal law with some mean value and variance.
The value of perception by agents of each other is positive or negative (implemented in the model as numerical values equal to +1 and -1). The distribution of perceptions over an ensemble of persons is implemented as a random variable specified by the probability of negative perception, the value of which is set by the control elements of the model interface. The numerical value of the probability equal to 0 corresponds to the case in which all persons positively perceive each other (the numerical value of the random variable is equal to 1, which corresponds to the positive perception of the other person by the individual).
The hierarchy is occupied with operational activity, the degree of intensity of which is set by the external parameter Difficulty. The level of productivity of each manager OAIndex is equal to the level of productivity of the department he leads and is the ratio of the sum of productivity of employees subordinate to the head to the level of complexity of the work Difficulty. An increase in the numerical value of Difficulty leads to a decrease in the OAIndex for all subdivisions of the hierarchy. The managerial meaning of the OAIndex indicator is the percentage of completion of the load specified for the hierarchy as a whole, i.e. the ratio of the actual performance of the structural subdivisions of the hierarchy to the required performance, the level of which is specified by the value of the Difficulty parameter.
…

ForagerNet3_Demography is a non-spatial ABM for exploring hunter-gatherer demography. Key methods represent birth, death, and marriage. The dependency ratio is an imporant variable in many economic decisions embedded in the methods.

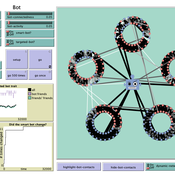
How do bots influence beliefs on social media? Why do beliefs propagated by social bots spread far and wide, yet does their direct influence appear to be limited?

This model extends Axelrod’s model for the dissemination of culture (1997), with a social bot agent–an agent who only sends information and cannot be influenced themselves. The basic network is a ring network with N agents connected to k nearest neighbors. The agents have a cultural profile with F features and Q traits per feature. When two agents interact, the sending agent sends the trait of a randomly chosen feature to the receiving agent, who adopts this trait with a probability equal to their similarity. To this network, we add a bot agents who is given a unique trait on the first feature and is connected to a proportion of the agents in the model equal to ‘bot-connectedness’. At each timestep, the bot is chosen to spread one of its traits to its neighbors with a probility equal to ‘bot-activity’.

The main finding in this model is that, generally, bot activity and bot connectedness are both negatively related to the success of the bot in spreading its unique message, in equilibrium. The mechanism is that very active and well connected bots quickly influence their direct contacts, who then grow too dissimilar from the bot’s indirect contacts to quickly, preventing indirect influence. A less active and less connected bot leaves more space for indirect influence to occur, and is therefore more successful in the long run.

A global model of the 1918-19 Influenza Pandemic. It can be run to match history or explore counterfactual questions about the influence of World War I on the dynamics of the epidemic. Explores two theories of the location of the initial infection.

This model simulates how collective self-organisation among individuals that manage irrigation resource collectively.

CINCH1 (Covid-19 INfection Control in Hospitals), is a prototype model of physical distancing for infection control among staff in University College London Hospital during the Covid-19 pandemic, developed at the University of Leeds, School of Geography. It models the movement of collections of agents in simple spaces under conflicting motivations of reaching their destination, maintaining physical distance from each other, and walking together with a companion. The model incorporates aspects of the Capability, Opportunity and Motivation of Behaviour (COM-B) Behaviour Change Framework developed at University College London Centre for Behaviour Change, and is aimed at informing decisions about behavioural interventions in hospital and other workplace settings during this and possible future outbreaks of highly contagious diseases. CINCH1 was developed as part of the SAFER (SARS-CoV-2 Acquisition in Frontline Health Care Workers – Evaluation to Inform Response) project
(https://www.ucl.ac.uk/behaviour-change/research/safer-sars-cov-2-acquisition-frontline-health-care-workers-evaluation-inform-response), funded by the UK Medical Research Council. It is written in Python 3.8, and built upon Mesa version 0.8.7 (copyright 2020 Project Mesa Team).

The model measures drivers of effectiveness of risk assessments in risk workshops regarding the correctness and required time. Specifically, we model the limits to information transfer, incomplete discussions, group characteristics, and interaction patterns and investigate their effect on risk assessment in risk workshops.

The model simulates a discussion in the context of a risk workshop with 9 participants. The participants use Bayesian networks to assess a given risk individually and as a group.

In the “World of Cows”, dairy farmers run their farms and interact with each other, the surrounding agricultural landscape, and the economic and political framework. The model serves as an exemplary case of an interdependent human-environment system.

With the model, users can analyze the influence of policies and markets on land use decisions of dairy farms. The land use decisions taken by farms determine the delivered ecosystem services on the landscape level. Users can choose a combination of five policy options and how strongly market prices fluctuate. Ideally, the choice of policy options fulfills the following three “political goals” 1) dairy farming stays economically viable, 2) the provision of ecosystem services is secured, and 3) government spending on subsidies is as low as possible.

The model has been designed for students to practice agent-based modeling and analyze the impacts of land use policies.

The model simulates tail biting behaviour in pigs and how they can turn into a biter and/or victim. The effect of a redirected motivation, behavioural changes in victims and preference to bite a lying pig on tail biting can be tested in the model