About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 98 results learning clear search
Peer reviewed Evolutionary Economic Learning Simulation: A Genetic Algorithm for Dynamic 2x2 Strategic-Form Games in Python
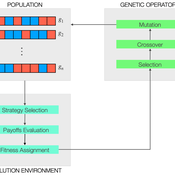
Vinicius Ferraz Thomas Pitz | Published Friday, April 08, 2022This project combines game theory and genetic algorithms in a simulation model for evolutionary learning and strategic behavior. It is often observed in the real world that strategic scenarios change over time, and deciding agents need to adapt to new information and environmental structures. Yet, game theory models often focus on static games, even for dynamic and temporal analyses. This simulation model introduces a heuristic procedure that enables these changes in strategic scenarios with Genetic Algorithms. Using normalized 2x2 strategic-form games as input, computational agents can interact and make decisions using three pre-defined decision rules: Nash Equilibrium, Hurwicz Rule, and Random. The games then are allowed to change over time as a function of the agent’s behavior through crossover and mutation. As a result, strategic behavior can be modeled in several simulated scenarios, and their impacts and outcomes can be analyzed, potentially transforming conflictual situations into harmony.
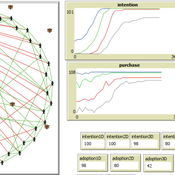
Diffusion of goods with multiple characteristics and price premiums
Pedro López Merino | Published Friday, February 18, 2022An agent-based model for the diffusion of innovations with multiple characteristics and price-premiums
The Effect of Different Governmental Pandemic Control Measures on the Spread of a Virus Disease
Chiara Letter | Published Wednesday, January 26, 2022In this model, the spread of a virus disease in a network consisting of school pupils, employed, and umemployed people is simulated. The special feature in this model is the distinction between different types of links: family-, friends-, school-, or work-links. In this way, different governmental measures can be implemented in order to decelerate or stop the transmission.
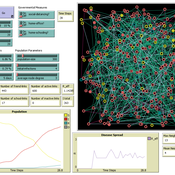
Peer reviewed Agent-based model to simulate equilibria and regime shifts emerged in lake ecosystems
no contributors listed | Published Tuesday, January 25, 2022(An empty output folder named “NETLOGOexperiment” in the same location with the LAKEOBS_MIX.nlogo file is required before the model can be run properly)
The model is motivated by regime shifts (i.e. abrupt and persistent transition) revealed in the previous paleoecological study of Taibai Lake. The aim of this model is to improve a general understanding of the mechanism of emergent nonlinear shifts in complex systems. Prelimnary calibration and validation is done against survey data in MLYB lakes. Dynamic population changes of function groups can be simulated and observed on the Netlogo interface.
Main functional groups in lake ecosystems were modelled as super-individuals in a space where they interact with each other. They are phytoplankton, zooplankton, submerged macrophyte, planktivorous fish, herbivorous fish and piscivorous fish. The relationships between these functional groups include predation (e.g. zooplankton-phytoplankton), competition (phytoplankton-macrophyte) and protection (macrophyte-zooplankton). Each individual has properties in size, mass, energy, and age as physiological variables and reproduce or die according to predefined criteria. A system dynamic model was integrated to simulate external drivers.
Set biological and environmental parameters using the green sliders first. If the data of simulation are to be logged, set “Logdata” as true and input the name of the file you want the spreadsheet(.csv) to be called. You will need create an empty folder called “NETLOGOexperiment” in the same level and location with the LAKEOBS_MIX.nlogo file. Press “setup” to initialise the system and “go” to start life cycles.
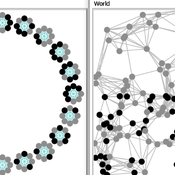
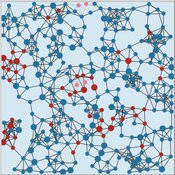
Two agent-based models of cooperation in dynamic groups and fixed social networks
Carlos A. de Matos Fernandes | Published Thursday, January 20, 2022Both models simulate n-person prisoner dilemma in groups (left figure) where agents decide to C/D – using a stochastic threshold algorithm with reinforcement learning components. We model fixed (single group ABM) and dynamic groups (bad-barrels ABM). The purpose of the bad-barrels model is to assess the impact of information during meritocratic matching. In the bad-barrels model, we incorporated a multidimensional structure in which agents are also embedded in a social network (2-person PD). We modeled a random and homophilous network via a random spatial graph algorithm (right figure).
FlipFlop1-ProMEERB: A coupled social-ecological model with a promotional mechanism for emergence of environmentally responsible behavior
Liliana Perez Saeed Harati Roberto Molowny-Horas | Published Friday, December 17, 2021At the heart of a study of Social-Ecological Systems, this model is built by coupling together two independently developed models of social and ecological phenomena. The social component of the model is an abstract model of interactions of a governing agent and several user agents, where the governing agent aims to promote a particular behavior among the user agents. The ecological model is a spatial model of spread of the Mountain Pine Beetle in the forests of British Columbia, Canada. The coupled model allowed us to simulate various hypothetical management scenarios in a context of forest insect infestations. The social and ecological components of this model are developed in two different environments. In order to establish the connection between those components, this model is equipped with a ‘FlipFlop’ - a structure of storage directories and communication protocols which allows each of the models to process its inputs, send an output message to the other, and/or wait for an input message from the other, when necessary. To see the publications associated with the social and ecological components of this coupled model please see the References section.
Peer reviewed Dynamic Value-based Cognitive Architectures
Bart de Bruin | Published Tuesday, November 30, 2021The intention of this model is to create an universal basis on how to model change in value prioritizations within social simulation. This model illustrates the designing of heterogeneous populations within agent-based social simulations by equipping agents with Dynamic Value-based Cognitive Architectures (DVCA-model). The DVCA-model uses the psychological theories on values by Schwartz (2012) and character traits by McCrae and Costa (2008) to create an unique trait- and value prioritization system for each individual. Furthermore, the DVCA-model simulates the impact of both social persuasion and life-events (e.g. information, experience) on the value systems of individuals by introducing the innovative concept of perception thermometers. Perception thermometers, controlled by the character traits, operate as buffers between the internal value prioritizations of agents and their external interactions. By introducing the concept of perception thermometers, the DVCA-model allows to study the dynamics of individual value prioritizations under a variety of internal and external perturbations over extensive time periods. Possible applications are the use of the DVCA-model within artificial sociality, opinion dynamics, social learning modelling, behavior selection algorithms and social-economic modelling.
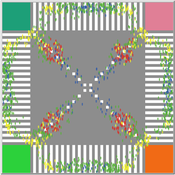
Pedestrian Scramble
Sho Takami Rami Lake Dara Vancea | Published Tuesday, November 30, 2021 | Last modified Tuesday, June 10, 2025This is a model intended to demonstrate the function of scramble crossings and a more efficient flow of pedestrian traffic with the presence of diagonal crosswalks.
Peer reviewed Virus Transmission with Super-spreaders
J M Applegate | Published Saturday, September 11, 2021A curious aspect of the Covid-19 pandemic is the clustering of outbreaks. Evidence suggests that 80\% of people who contract the virus are infected by only 19% of infected individuals, and that the majority of infected individuals faile to infect another person. Thus, the dispersion of a contagion, $k$, may be of more use in understanding the spread of Covid-19 than the reproduction number, R0.
The Virus Transmission with Super-spreaders model, written in NetLogo, is an adaptation of the canonical Virus Transmission on a Network model and allows the exploration of various mitigation protocols such as testing and quarantines with both homogenous transmission and heterogenous transmission.
The model consists of a population of individuals arranged in a network, where both population and network degree are tunable. At the start of the simulation, a subset of the population is initially infected. As the model runs, infected individuals will infect neighboring susceptible individuals according to either homogenous or heterogenous transmission, where heterogenous transmission models super-spreaders. In this case, k is described as the percentage of super-spreaders in the population and the differing transmission rates for super-spreaders and non super-spreaders. Infected individuals either recover, at which point they become resistant to infection, or die. Testing regimes cause discovered infected individuals to quarantine for a period of time.
Peer reviewed Price Evolution with Expectations
J M Applegate Gesine Steudel Armin Haas Carlo Jaeger | Published Friday, September 10, 2021The Price Evolution with Expectations model provides the opportunity to explore the question of non-equilibrium market dynamics, and how and under which conditions an economic system converges to the classically defined economic equilibrium. To accomplish this, we bring together two points of view of the economy; the classical perspective of general equilibrium theory and an evolutionary perspective, in which the current development of the economic system determines the possibilities for further evolution.
The Price Evolution with Expectations model consists of a representative firm producing no profit but producing a single good, which we call sugar, and a representative household which provides labour to the firm and purchases sugar.The model explores the evolutionary dynamics whereby the firm does not initially know the household demand but eventually this demand and thus the correct price for sugar given the household’s optimal labour.
The model can be run in one of two ways; the first does not include money and the second uses money such that the firm and/or the household have an endowment that can be spent or saved. In either case, the household has preferences for leisure and consumption and a demand function relating sugar and price, and the firm has a production function and learns the household demand over a set number of time steps using either an endogenous or exogenous learning algorithm. The resulting equilibria, or fixed points of the system, may or may not match the classical economic equilibrium.
Displaying 10 of 98 results learning clear search