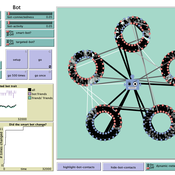
How do bots influence beliefs on social media? Why do beliefs propagated by social bots spread far and wide, yet does their direct influence appear to be limited?

This model extends Axelrod’s model for the dissemination of culture (1997), with a social bot agent–an agent who only sends information and cannot be influenced themselves. The basic network is a ring network with N agents connected to k nearest neighbors. The agents have a cultural profile with F features and Q traits per feature. When two agents interact, the sending agent sends the trait of a randomly chosen feature to the receiving agent, who adopts this trait with a probability equal to their similarity. To this network, we add a bot agents who is given a unique trait on the first feature and is connected to a proportion of the agents in the model equal to ‘bot-connectedness’. At each timestep, the bot is chosen to spread one of its traits to its neighbors with a probility equal to ‘bot-activity’.

The main finding in this model is that, generally, bot activity and bot connectedness are both negatively related to the success of the bot in spreading its unique message, in equilibrium. The mechanism is that very active and well connected bots quickly influence their direct contacts, who then grow too dissimilar from the bot’s indirect contacts to quickly, preventing indirect influence. A less active and less connected bot leaves more space for indirect influence to occur, and is therefore more successful in the long run.

This is a simulation of an insurance market where the premium moves according to the balance between supply and demand. In this model, insurers set their supply with the aim of maximising their expected utility gain while operating under imperfect information about both customer demand and underlying risk distributions.

There are seven types of insurer strategies. One type follows a rational strategy within the bounds of imperfect information. The other six types also seek to maximise their utility gain, but base their market expectations on a chartist strategy. Under this strategy, market premium is extrapolated from trends based on past insurance prices. This is subdivided according to whether the insurer is trend following or a contrarian (counter-trend), and further depending on whether the trend is estimated from short-term, medium-term, or long-term data.

Customers are modelled as a whole and allocated between insurers according to available supply. Customer demand is calculated according to a logit choice model based on the expected utility gain of purchasing insurance for an average customer versus the expected utility gain of non-purchase.

The original Ache model is used to explore different distributions of resources on the landscape and it’s effect on optimal strategies of the camps on hunting and camp movement.

This is a simulation model to explore possible outcomes of the Port of Mars cardgame. Port of Mars is a resource allocation game examining how people navigate conflicts between individual goals and common interests relative to shared resources. The game involves five players, each of whom must decide how much of their time and effort to invest in maintaining public infrastructure and renewing shared resources and how much to expend in pursuit of their individual goals. In the game, “Upkeep” is a number that represents the physical health of the community. This number begins at 100 and goes down by twenty-five points each round, representing resource consumption and wear and tear on infrastructure. If that number reaches zero, the community collapses and everyone dies.

This is an agent-based model of a simple insurance market with two types of agents: customers and insurers. Insurers set premium quotes for each customer according to an estimation of their underlying risk based on past claims data. Customers either renew existing contracts or else select the cheapest quote from a subset of insurers. Insurers then estimate their resulting capital requirement based on a 99.5% VaR of their aggregate loss distributions. These estimates demonstrate an under-estimation bias due to the winner’s curse effect.

This model aims to investigate how different type of learning (social system) and disturbance specific attributes (ecological system) influence adoption of treatment strategies to treat the effects of ecological disturbances.

A model to show the effects of flood risk on a housing market; the role of flood protection for risk reduction; the working of the existing public-private flood insurance partnership in the UK, and the proposed scheme ‘Flood Re’.

A NetLogo ABM developed to explore unarmed resistance to an active shooter. The landscape is a generalized open outdoor area. Parameters enable the user to set shooter armament and control for assumptions with regard to shooter accuracy.

The model simulates the national Campaign-Based Watershed Management program of Ethiopia. It includes three agents (farmers, Kebele/ village administrator, extension workers) and the physical environment that interact with each other. The physical environment is represented by patches (fields). Farmers make decisions on the locations of micro-watersheds to be developed, participation in campaign works to construct soil and water conservation structures, and maintenance of these structures. These decisions affect the physical environment or generate model outcomes. The model is developed to explore conditions that enhance outcomes of the program by analyzing the effect on the area of land covered and quality of soil and water conservation structures of (1) enhancing farmers awareness and motivation, (2) establishing and strengthening micro-watershed associations, (3) introducing alternative livelihood opportunities, and (4) enhancing the commitment of local government actors.

Like many developing countries, Nigeria is faced with a number of tradeoffs that pit rapid economic development against environmental preservation. Environmentally sustainable, “green” economic development is slower, more costly, and more difficult than unrestricted, unregulated economic growth. The mathematical model that we develop in this code suggests that widespread public awareness of environmental issues is insufficient to prevent the tendency towards sacrificing the environment for the sake of growth. Even if people have an understanding of negative impacts and always choose to act in their own self-interest, they may still act collectively in such a way as to bring down the quality of life for the entire society. We conclude that additional actions must be taken besides raising public awareness of the environmental problem.