About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 288 results for "Ned Wellman" clear search
This model extends the original Artifical Anasazi (AA) model to include individual agents, who vary in age and sex, and are aggregated into households. This allows more realistic simulations of population dynamics within the Long House Valley of Arizona from AD 800 to 1350 than are possible in the original model. The parts of this model that are directly derived from the AA model are based on Janssen’s 1999 Netlogo implementation of the model; the code for all extensions and adaptations in the model described here (the Artificial Long House Valley (ALHV) model) have been written by the authors. The AA model included only ideal and homogeneous “individuals” who do not participate in the population processes (e.g., birth and death)–these processes were assumed to act on entire households only. The ALHV model incorporates actual individual agents and all demographic processes affect these individuals. Individuals are aggregated into households that participate in annual agricultural and demographic cycles. Thus, the ALHV model is a combination of individual processes (birth and death) and household-level processes (e.g., finding suitable agriculture plots).
As is the case for the AA model, the ALHV model makes use of detailed archaeological and paleoenvironmental data from the Long House Valley and the adjacent areas in Arizona. It also uses the same methods as the original model (from Janssen’s Netlogo implementation) to estimate annual maize productivity of various agricultural zones within the valley. These estimates are used to determine suitable locations for households and farms during each year of the simulation.
Artificial Long House Valley-Black Mesa
Lisa Sattenspiel Amy Warren | Published Thursday, March 19, 2020This model is an extension of the Artificial Long House Valley (ALHV) model developed by the authors (Swedlund et al. 2016; Warren and Sattenspiel 2020). The ALHV model simulates the population dynamics of individuals within the Long House Valley of Arizona from AD 800 to 1350. Individuals are aggregated into households that participate in annual agricultural and demographic cycles. The present version of the model incorporates features of the ALHV model including realistic age-specific fertility and mortality and, in addition, it adds the Black Mesa environment and population, as well as additional methods to allow migration between the two regions.
As is the case for previous versions of the ALHV model as well as the Artificial Anasazi (AA) model from which the ALHV model was derived (Axtell et al. 2002; Janssen 2009), this version makes use of detailed archaeological and paleoenvironmental data from the Long House Valley and the adjacent areas in Arizona. It also uses the same methods as the original AA model to estimate annual maize productivity of various agricultural zones within the Long House Valley. A new environment and associated methods have been developed for Black Mesa. Productivity estimates from both regions are used to determine suitable locations for households and farms during each year of the simulation.
Peer reviewed Evolution of Cooperation in Asymmetric Commons Dilemmas
Marco Janssen Nathan Rollins | Published Friday, August 20, 2010 | Last modified Saturday, April 27, 2013This model can be used to explore under which conditions agents behave as observed in field experiments on irrigation games.
Linear Threshold
Kaushik Sarkar | Published Saturday, November 03, 2012 | Last modified Saturday, April 27, 2013NetLogo implementation of Linear Threshold model of influence propagation.
Will it spread or not? The effects of social influences and network topology on innovation diffusion
Sebastiano Delre | Published Monday, October 24, 2011 | Last modified Saturday, April 27, 2013This models simulates innovation diffusion curves and it tests the effects of the degree and the direction of social influences. This model replicates, extends and departs from classical percolation models.
Land-Livelihood Transitions
Nicholas Magliocca Daniel G Brown Erle C Ellis | Published Monday, September 09, 2013 | Last modified Friday, September 13, 2013Implemented as a virtual laboratory, this model explores transitions in land-use and livelihood decisions that emerge from changing local and global conditions.
This is a social trust model for investigating the social relationships and social networks in the real world and in social media.
A model to explore the link between the gender-gap reversal in education and relative divorce risks
Jan Van Bavel Christine Schnor André Grow | Published Thursday, June 30, 2016 | Last modified Wednesday, September 13, 2017This model explores a social mechanism that links the reversal of the gender gap in education with changing patterns in relative divorce risks in 12 European countries.
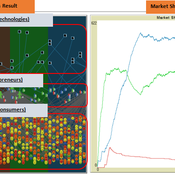
The simulation on the study of the optimal business strategy with the interaction between technologies and consumers.
sej-yoo | Published Monday, June 27, 2022 | Last modified Monday, July 04, 2022HOW IT WORKS
This model consists of three agents, and each agent type operates per business theories as below.
a. New technologies(Tech): It evolves per sustaining or disruptive technology trajectory with the constraint of project management triangle (Scope, Time, Quality, and Cost).
b. Entrepreneurs(Entre): It builds up the solution by combining Tech components per its own strategy (Exploration, Exploitation, or Ambidex).
c. Consumer(Consumer): It selects the solution per its own preference due to Diffusion of innovation theory (Innovators, Early Adopters, Early Majority, Late Majority, Laggards)
…
Evolutionary Model of Subculture Choice
Diogo Alves | Published Monday, December 19, 2022This is an original model of (sub)culture diffusion.
It features a set of agents (dubbed “partygoers”) organized initially in clusters, having properties such as age and a chromosome of opinions about 6 different topics. The partygoers interact with a set of cultures (also having a set of opinions subsuming those of its members), in the sense of refractory or unhappy members of each setting about to find a new culture and trading information encoded in the genetic string (originally encoded as -1, 0, and 1, resp. a negative, neutral, and positive opinion about each of the 6 traits/aspects, e.g. the use of recreational drugs). There are 5 subcultures that both influence (through the aforementioned genetic operations of mutation and recombination of chromosomes simulating exchange of opinions) and are influenced by its members (since a group is a weighted average of the opinions and actions of its constituents). The objective of this feedback loop is to investigate under which conditions certain subculture sizes emerge, but the model is open to many other kinds of explorations as well.
Displaying 10 of 288 results for "Ned Wellman" clear search