About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 983 results for "Chantal van Esch" clear search
Narragansett Bay (RI) Recreational Fishery ABM
Tyler Pavlowich Anne Innes-Gold Margaret Heinichen M. Conor McManus Jason McNamee Jeremy Collie Austin Humphries | Published Monday, June 21, 2021This model is based on the Narragansett Bay, RI recreational fishery. The two types of agents are piscivorous fish and fishers (shore and boat fishers are separate “breeds”). Each time step represents one week. Open season is weeks 1-26, assuming fishing occurs during half the year. At each weekly time step, fish agents grow, reproduce, and die. Fisher agents decide whether or not to fish based on their current satisfaction level, and those that do go fishing attempt to catch a fish. If they are successful, they decide whether to keep or release the fish. In our publication, this model was linked to an Ecopath with Ecosim food web model where the commercial harvest of forage fish affected the biomass of piscivorous fish - which then became the starting number of piscivorous fish for this ABM. The number of fish caught in a season of this ABM was converted to a fishing pressure and input back into the food web model.
Adaptive model of a consumer advice network
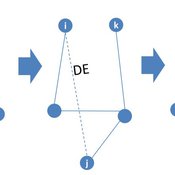
Peng Shao | Published Monday, May 14, 2018In the consumer advice network, users with connections can interact with each other, and the network topology will change during the opinion interaction. When the opinion distance from i to j is greater than the confidence threshold, the two consumers cannot exchange opinions, and the link between them will disconnect with probability DE. Then, a link from node i to node k is established with probability CE and node i learning opinion from node k.
Informal Information Transmission Networks among Medieval Genoese Investors
Christopher Frantz | Published Wednesday, October 09, 2013 | Last modified Thursday, October 24, 2013This model represents informal information transmission networks among medieval Genoese investors used to inform each other about cheating merchants they employed as part of long-distance trade operations.
RecovUS: An Agent-Based Model of Post-Disaster Household Recovery
Saeed Moradi | Published Thursday, July 30, 2020The purpose of this model is to explain the post-disaster recovery of households residing in their own single-family homes and to predict households’ recovery decisions from drivers of recovery. Herein, a household’s recovery decision is repair/reconstruction of its damaged house to the pre-disaster condition, waiting without repair/reconstruction, or selling the house (and relocating). Recovery drivers include financial conditions and functionality of the community that is most important to a household. Financial conditions are evaluated by two categories of variables: costs and resources. Costs include repair/reconstruction costs and rent of another property when the primary house is uninhabitable. Resources comprise the money required to cover the costs of repair/reconstruction and to pay the rent (if required). The repair/reconstruction resources include settlement from the National Flood Insurance (NFI), Housing Assistance provided by the Federal Emergency Management Agency (FEMA-HA), disaster loan offered by the Small Business Administration (SBA loan), a share of household liquid assets, and Community Development Block Grant Disaster Recovery (CDBG-DR) fund provided by the Department of Housing and Urban Development (HUD). Further, household income determines the amount of rent that it can afford. Community conditions are assessed for each household based on the restoration of specific anchors. ASNA indexes (Nejat, Moradi, & Ghosh 2019) are used to identify the category of community anchors that is important to a recovery decision of each household. Accordingly, households are indexed into three classes for each of which recovery of infrastructure, neighbors, or community assets matters most. Further, among similar anchors, those anchors are important to a household that are located in its perceived neighborhood area (Moradi, Nejat, Hu, & Ghosh 2020).
A Consumer in the Jungle of Product Differentiation
Alessandro Pluchino Andrea Rapisarda Alessio Emanuele Biondo Alfio Giarlotta | Published Tuesday, December 22, 2015Building upon the distance-based Hotelling’s differentiation idea, we describe the behavioral experience of several prototypes of consumers, who walk a hypothetical cognitive path in an attempt to maximize their satisfaction.
How does the world population adapt its policies on energy when it is confronted with a climate change? This model combines a climate-economy model with adaptive agents.
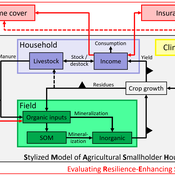
SMASH: Stylized Model of Agricultural Smallholder Households
Tim Williams | Published Tuesday, December 08, 2020The SMASH model is an agent-based model of rural smallholder households. It models households’ evolving income and wealth, which they earn through crop sales. Wealth is carried in the form of livestock, which are grazed on an external rangeland (exogenous) and can be bought/sold as investment/coping mechanisms. The model includes a stylized representation of soil nutrient dynamics, modeling the inflows and outflows of organic and inorganic nitrogen from each household’s field.
The model has been applied to assess the resilience-enhancing effects of two different farm-level adaptation strategies: legume cover cropping and crop insurance. These two strategies interact with the model through different mechanims - legume cover cropping through ecological mechanisms and crop insurance through financial mechanisms. The model can be used to investigate the short- and long-term effects of these strategies, as well as how they may differently benefit different types of household.
World of Cows - Exploring land-use policies for a dairy-farm world (teaching modeling complex human-environment systems)
Maria Haensel Thomas Michael Schmitt Jakob Bogenreuther | Published Wednesday, January 11, 2023In the “World of Cows”, dairy farmers run their farms and interact with each other, the surrounding agricultural landscape, and the economic and political framework. The model serves as an exemplary case of an interdependent human-environment system.
With the model, users can analyze the influence of policies and markets on land use decisions of dairy farms. The land use decisions taken by farms determine the delivered ecosystem services on the landscape level. Users can choose a combination of five policy options and how strongly market prices fluctuate. Ideally, the choice of policy options fulfills the following three “political goals” 1) dairy farming stays economically viable, 2) the provision of ecosystem services is secured, and 3) government spending on subsidies is as low as possible.
The model has been designed for students to practice agent-based modeling and analyze the impacts of land use policies.
The Mobility Model
Emilie Lindkvist | Published Wednesday, September 27, 2017 | Last modified Friday, October 06, 2017The Mobility Model is a model of a small-scale fishery with the purpose to study the movement of fishers between different sub-regions within a larger region, as they move between different regions to fish.
Peer reviewed Casting: A Bio-Inspired Method for Restructuring Machine Learning Ensembles
Colin Lynch Bryan Daniels | Published Thursday, September 18, 2025The wisdom of the crowd refers to the phenomenon in which a group of individuals, each making independent decisions, can collectively arrive at highly accurate solutions—often more accurate than any individual within the group. This principle relies heavily on independence: if individual opinions are unbiased and uncorrelated, their errors tend to cancel out when averaged, reducing overall bias. However, in real-world social networks, individuals are often influenced by their neighbors, introducing correlations between decisions. Such social influence can amplify biases, disrupting the benefits of independent voting. This trade-off between independence and interdependence has striking parallels to ensemble learning methods in machine learning. Bagging (bootstrap aggregating) improves classification performance by combining independently trained weak learners, reducing bias. Boosting, on the other hand, explicitly introduces sequential dependence among learners, where each learner focuses on correcting the errors of its predecessors. This process can reinforce biases present in the data even if it reduces variance. Here, we introduce a new meta-algorithm, casting, which captures this biological and computational trade-off. Casting forms partially connected groups (“castes”) of weak learners that are internally linked through boosting, while the castes themselves remain independent and are aggregated using bagging. This creates a continuum between full independence (i.e., bagging) and full dependence (i.e., boosting). This method allows for the testing of model capabilities across values of the hyperparameter which controls connectedness. We specifically investigate classification tasks, but the method can be used for regression tasks as well. Ultimately, casting can provide insights for how real systems contend with classification problems.
Displaying 10 of 983 results for "Chantal van Esch" clear search